
I can explain digital logic down to the electron in a MOSFET, but I can't come close to the same with quantum computing. This newsletter is a journal of my quest to learn the fundamentals of quantum computing and explain them on a human level.
Welcome to the Quantum Edge newsletter. Join me in my year-long journey into the weirdness that is quantum computing.
Issue 13.0, November 21, 2025
In today’s newsletter: A review of conventional computer number storage and an Introduction to quantum computer numbers - How superposition allows storing bigger numbers than conventional computers
Quantum computers, at a high level, operate much like conventional digital computers. They take data in, use algorithms to process information, reach conclusions, and send data out. The important computational differences between a laptop computer and a quantum computer are in how those algorithms are built and run and how the data is stored.
With a conventional digital computer, as I’ve written about before, memory and logic circuits store on or off states and use logic to combine or interpret those on or off states. They operate based on the bit, which is a single digital switch. These switches can have a small voltage charge or not have a charge. Larger circuits put charge into that part or drain it out. Collections of these simple circuits (billions of circuits in a single chip) are combined to create very powerful computers.
Quantum computers rely on the qubit properties of spin, superposition, and quantum entanglement to store and compute information. Spin down is a 0 and spin up is a 1. Today’s quantum computers put a few dozen to a few thousand qubits per chip. In the future, quantum computers will put billions of qubits together to create computers powerful enough to seem like science fiction.
So far, quantum computers don’t sound much different than conventional computers. We’re about to change that. Quantum computers can store and work on numbers much larger for a given number of qubits than conventional computers can with the same number of bits.
Before we start trying to understand qubits and how they can store bigger numbers, it will be helpful to review conventional computer numbers. We will look at how numbers are stored in bits within conventional computers and then do the same for qubits within quantum computers.
How Numbers are Represented
A number is just a set of straight or squiggly lines that we have been told have meaning. If you have a thing, you have one of those things. Get another and you have two. Another and you have three. Take all of them away and you have none of those things. Numbers are what we use to make those concepts less confusing.
Our common base-10 number system has ten different shaped symbols, called numerals (the squiggly lines), to choose from: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. There are ten choices because we have ten fingers. We sometimes call numerals digits because fingers are sometimes called digits, and fingers were humanity’s first counting devices. We get bigger numbers by putting together different groupings of digits (e.g., 741, 2708, 7400). We call it a base-10 number system because there are 10 different numerals/digits. Ten fingers, ten digits, base-10 number system. That’s the rule.
But here’s the thing. Rules are just made up.
We could just as easily have ended up with a base-60 number system. The ancient Egyptians and Babylonians had the same ten fingers as we do, but they counted differently with their fingers. They used their thumb to count on the segments of each of the other four fingers in their hand. That’s why we have 12 hours before noon and 12 hours after noon (Egyptians gave the day 12 hours and the night 12 hours). It’s also why there are 12 inches in a foot and three feet to a yard (three segments in a finger for three feet in a yard).
Counting with finger segments
Count to 12 on one hand, then raise one finger on your other hand and count to 12 again. Do this for all five fingers on the other hand and you have counted to 60. That’s easier than trying to count to 100 on your hands with our base 10 system. This is where we get 60 minutes in an hour and 60 seconds in a minute.
Fun fact: The word “minute” comes from a Latin root “pers minuta prima” meaning “the first small part” of the hour. Seconds are the “second small part” of the hour.
Someone just made that all up. The person who invents or discovers something usually gets to make up the names and the rules. If it can be explained to others and it works, the system sticks around. Math works pretty well in both base-10 and base-60. I’m not sure why base-60 didn’t stick around, but things were messy a few thousand years ago and humanity forgot a fair amount of stuff for a while.
Fun fact: Between the time of Egyptians and Babylonians, and now, the Romans came in and messed up numbers for a bit. The Romans didn’t have anything like a 0 to mean “none”, and they used groupings of I, V, X, L, C, D, and M to count. Counting one to ten in Roman numerals looks like this: I, II, III, IV, V, VI, VII, VIII, IX, X. It looks great on a decorative clock but can’t be used with anything but the simplest math. That may, in fact, be why we don’t use base-60 today. We forgot it during Roman times and came out of that era too tired to do anything but count to ten. Could be.
Somewhere along the line, the base ten system was adopted, and we seem to be stuck with it - along with a few remnants of base-60, like 12 hours and 60 minutes.
Computers don’t have ten fingers, nor do they have three segments in each finger. They only have on/off switches. The on/off switch is effectively one finger. Finger down is 0 and finger up is 1. Conventional digital computers and quantum computers can’t count or do math with anything other than combinations of 0 and 1. The rest of the numerals through 9 only come into play on keyboards and display devices. Computers translate both ways so they can internally work with base-2 and we can work with base-10 externally.
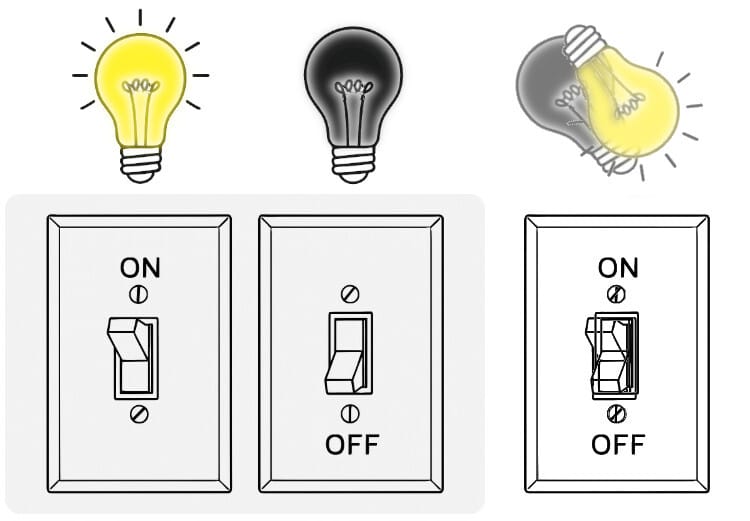
Figure 1. Light switches and lights to represent digital bits on and off (left and center), and a qubit in superposition (right) representing both on and off.
If bits and qubits can only be 0 and/or 1, how can computers of any type represent larger numbers and letters?
Representing Bigger Numbers With Just 0 and 1
Computers have a lot of bits side by side. This allows multiple bits of 0 and 1 to be grouped into patterns. The more bits side by side, the more patterns a computer can make out of 0 and 1. As was discussed in issue 9, eight bits side by side is called a byte. When you group multiple bytes side by side, we call that a word. Most modern computers do math with words that have eight bytes, or 64 bits side by side. The biggest number you can hold with 64 bits is 18,446,744,073,709,551,615. Computers use software tricks to hold even bigger numbers, but those tricks take time and slow the computer processing down.
In a computer, there are only two choices as we’ve said before. Off and on can be thought of as two digits. Only having two digits means they can only count in a base-2 system. We also call base-2 “binary” because in Latin, “binarius” means “consisting of two.” Like with base-10, bigger numbers are just different patterns made with the available digits - 0 and 1 in the case of base-2 numbers.
If we only had 1, a base-1 system, to work with and no 0, we would represent numbers by putting more and more 1s side by side:
= 0. No 1s allows you to represent 0.
1 = 1. One 1 allows you to count to 1
11 = 2. Two 1s allow you to count to 2
111 = 3. Three 1s allow you to count to 3
1111 = 4. Four 1s allow you to count to 4
11111 = 5. Five 1s allow you to count to five
And so on…
But computers do have both 0 and 1 to work with. That means we must come up with a set of patterns that use both numerals. With both, a single bit allows us to count from 0 to 1. Two bits allow us to count from 0 to 3 (see the table in figure 2 below). Three bits will allow us to count from 0 to 7.
1 bit | 0 = 0 | 1 = 1 | ||||||
2 bits | 00 = 0 | 01 = 1 | 10 = 2 | 11 = 3 | ||||
3 bits | 000 = 0 | 001 = 1 | 010 = 2 | 011 = 3 | 100 = 4 | 101 = 5 | 110 = 6 | 111 = 7 |
Figure 2. Numbers that can be represented with increasing number of bits
The arrangement of the 0s and 1s in those counting patterns may look random but it is not. In our base-10 number system, we first count with all of the numerals (0 - 9) until we run out of different numerals. Then we put a 1 to the left of the single numeral and run through 0 - 9 nine again. This gives us 10 - 19. Then we go 20 - 19 until, at 99, we are again all out of different numerals. We put a 1 to the left of 99 and start over with 0 in the other spots: 100.
We do the same in base-2 (binary), except the only numerals we have to use are 0 and 1. We put down a 0 and then a 1. After that there are no more numerals, so we put a 1 to the left and start over at 0 on the right: 10. Count again and the zero on the right goes up to 1: 11. Now you are out of different numerals again, so you put a 1 on the left and start over with 00 on the right: 100.
Keep repeating that pattern and you get 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111. The illustration below shows counting from 0 through 4 using our lightbulb as binary bit metaphor.
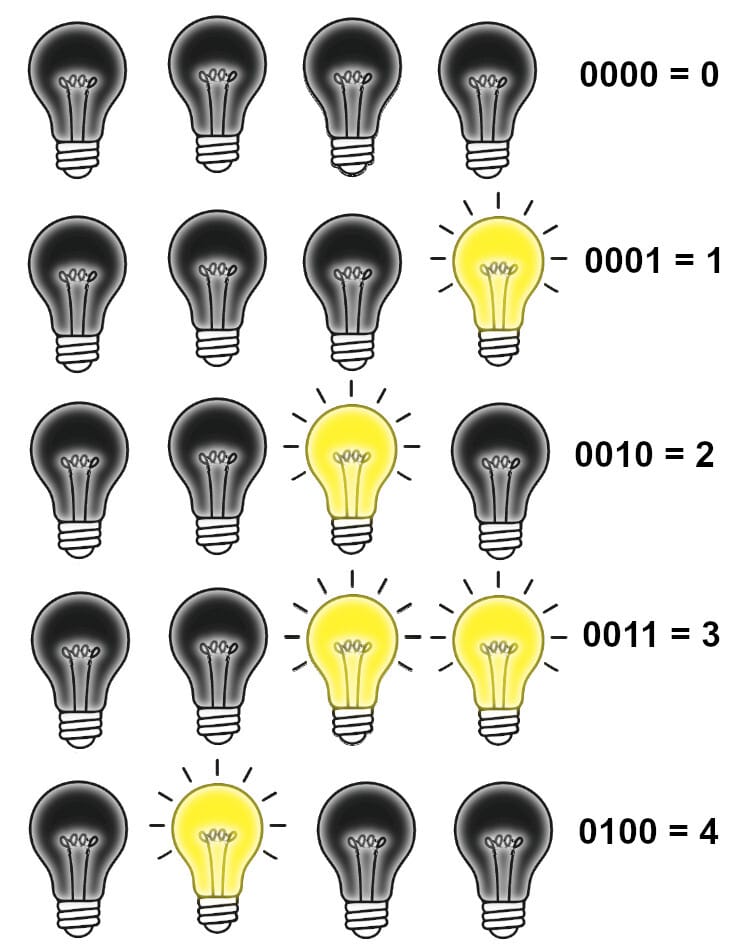
Figure 3. Counting with patterns of lightbulbs
Each bit that you add to doubles the number of possible combinations of values that can be represented by that word. One bit gives two combinations, two bits gives four combinations, three bits gives eight combinations, four bits gives sixteen, and so on.
Quantum Stuff: Representing Numbers with Qubits
While regular computer bits use an electric voltage charge to represent the value 1 and a lack of charge to represents 0, quantum computers use the quantum spin state of a qubit to represent numbers. In a quantum computer qubit, a spin down state represents 0 and a spin up state represents 1. Two qubits can give you four possible patterns of 0 and 1 states, just like two conventional bits. Three qubits give eight patterns, and so on. So far, this doesn’t seem any different from a conventional digital computer.
Just wait…
Inside a conventional computer, if a bit has a charge, it is always 1. Without charge, always 0. There is nothing in between. You can read the bit as often as you want and the value doesn’t change until the circuit takes action and adds or drains away the charge.
A quantum computer qubit at work can be both 0 and 1 at the same time because of superposition. When you read the value, superposition collapses and the qubit value becomes either 0 or 1. You get to read it once and then the state vanishes. It has value when you read it but not before or after. Yikes.
Quantum computers use conventional computers to control and read the qubits, so once read, the qubit loses its value, but it’s stored in the conventional computer for use later.
To restate: Before a qubit is read, it is in a state of superposition, which means that a single qubit can represent two states at the same time. While a regular bit can be either 0 or 1, a qubit can be both 0 and 1 simultaneously (you may want to go back and read issue 10 for a refresher on superposition). Two conventional bits can be any one of four different patterns of 0 or 1 but two qubits can hold all four combinations of 0 and 1 at the same time.
A conventional computer would need eight bits to hold all four combinations. Put the possible combinations of two-bit patterns (00, 01, 10, and 11) together and it would be stored in a conventional computer as 00011011. Two qubits will essentially hold all four of those patterns in just the two qubits. Three qubits can hold the same number of binary patterns as 24 conventional bits.
A Key Quantum Advantage
Finally, we are getting to one of the key advantages of quantum computers over conventional computers: space to store numbers. Since superposition allows qubits to hold both 0 and 1 simultaneously, they can hold significantly more numbers with fewer qubits than bits. Figure 4, below, continues our lightbulb metaphor to show how many bits vs. qubits are required to hold numbers.
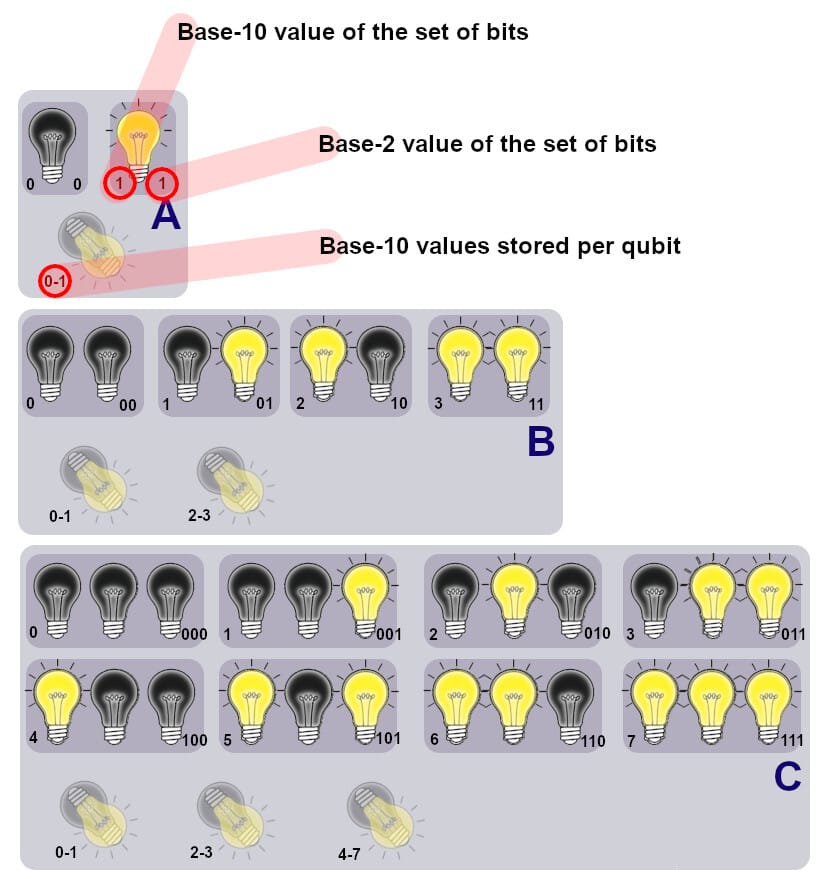
Figure 4. How qubits can store more numbers with fewer qubits than bits
If you want to store 0 or 1, you need one bit. If you want to store both 0 and 1, you need two bits. When storing in a quantum computer, a single qubit can do all of that. It can store both 0 and 1 at the same time. Figure 4 A shows the use two bits to store two different digit patterns and one qubit to store the same two patterns.
To store larger numbers, you have to group more bits and more qubits. If you want to store all of the different numbers that can be made with two bits, you need 8 total bits (00 01 10 11). Figure 4 B shows eight lightbulbs representing eight bits holding all of these patterns simultaneously. Only two qubits are required to hold the same amount of numbers.
Figure 4 C shows the bit and qubit storage amounts needed for the eight different patterns you can make with three bits. It takes 24 bits but only 3 qubits to store all eight patterns. The first qubit gets you enough storage to hold base-10 number 0 through 1. With the second qubit, you can now hold base-10 numbers 0 through 3. Adding a third qubit gives you the ability to store all base-10 numbers between 0 and 7.
To Summarize
You can hold any one of the numbers 0 - 7 (as shown in figure 4) with three conventional bits. It takes 24 conventional bits to store all of the numbers 0 - 7 simultaneously.
You can hold all of the numbers between 0 and 7 simultaneously with three qubits. With four bits (not shown in the figure), you can hold any one of numbers between 0 and 15. It would take 64 bits to hold all of the numbers 0 through 15 simultaneously. Four qubits can store all the numbers from 0 through 15.
1 qubit gets you the same storage as 2 bits
2 qubits get you the same storage as 8 bits
3 qubits get you the same storage as 24 bits
4 qubits get you the same storage as 64 bits
You can see how a small number of qubits can hold a large number of numbers simultaneously.
A Practical Example
Sorry. I think you’ve had enough for today. (or maybe I have)
Next issue, I will start out with an example illustrating the difference qubits make in a basic math problem. The example I use involves factoring prime number-based encryption keys. It’s a good example, because prime numbers are used in encryption to keep our banking data (and many other things) safe. One of the hyped-up fears of quantum computers is that they will soon be able to break all common encryption schemes making all of our data instantly vulnerable to criminals. I’ll give you a window into how that can happen.
If nothing were being done to solve the problem, fear would be a good option. However, like with the Y2K problem back at the turn of the century, the industry is working hard to fix the problem before quantum computers are real enough to break all encryption.
Everything Deserves a Name
One last thing before we go -
Everything deserves a name and like the rules I spoke of earlier, names are made up. Someone got to pick a name for qubits. In fact, they picked more than one name. Science things often get more than one name. Usually, there is a name for human descriptive language and a different name for use in the language of math.
“Qubit” is the human descriptive language name. It has a math name also. The math name is a Greek alphabet character: Ψ, called psi. It is pronounced like “sigh.” In words, we call it a qubit. In math, we refer to it as: Ψ.
Now, An Easy Way to Review or Catch Up
New to the Quantum Edge newsletter?
Thinking about re-reading it but want a more transportable format?
I’ve wrapped the first ten issues of The Quantum Edge newsletter into book form. The collection, called “The Quantum Computing Anthology, Volume 1”, is now available in Kindle and paperback on Amazon. The book collects issues 1 through 10 and has some additional material and edits for continuity and clarity. I will add another volume to the series every ten newsletter issues, so look for Volume 2 (newsletter issues 11 - 20) in early 2026.
You can order the Kindle and paperback editions on Amazon: The Quantum Computing Anthology, Volume 1
That’s All for Now
Check your email box Thursday - probably. (Okay, some of these weekly issues have come out on Friday, or not at all. But, in a quantum world, how can you tell?)
If you received this newsletter as a forward and wish to subscribe yourself, you can do so at quantumedge.today/subscribe.

Quantum Computing Archive
Below are a few articles on developments in quantum computing:
All About Circuits, Mar 2025: What Does Security Look Like in a Post-Quantum World? ST Looks Ahead
Max Maxfield’s Cool Beans blog, Dec 2024: Did AI Just Prove Our Understanding of “Quantum” is Wrong?
All About Circuits, Dec 2024: IBM Demonstrates First ‘Multi-Processor’ for Quantum Processing
All About Circuits, Aug 2024: Japan’s NTT-Docomo Uses Quantum Computing to Optimize Cell Networks
Independent Resources
Developments in quantum computing from the sources
Microsoft quantum news, Feb 2025: Majorana 1 chip news
Following are some of the quantum computing resources that I regularly visit or have found to be useful:
Quantum computing at Intel. Read about Intel’s take on quantum computing
IBM Quantum Platform. Information about and access to IBM's quantum computing resources. quantum.ibm.com
Google Quantum AI. Not as practical as the IBM site, but a good resource none the less. quantumai.google.com
IONQ developer resources and documentation. docs.ionq.com
About Positive Edge LLC
Positive Edge is the consulting arm of Duane Benson, Tech journalist, Futurist, Entrepreneur. Positive Edge is your conduit to decades of leading-edge technology development, management and communications expertise.


